|
ΚΕΦΑΛΑΙΟ 1ο:
Βασικά
Στοιχεία Τροχιακής Μηχανικής
Α. Εισαγωγή
- Τι είναι ταχύτητα διαφυγής και από τι
εξαρτάται;
Ρίχνοντας μια πέτρα πλάγια προς τα πάνω, παρατηρούμε ότι αυτή εκτελεί καμπύλη διαδρομή και μετά από κάποιο χρονικό διάστημα πέφτει στο έδαφος. Η τροχιά που διαγράφει εξαρτάται μόνο από τις αρχικές συνθήκες (αρχική ταχύτητα και γωνία βολής). Το ερώτημα που τίθεται είναι αν υπάρχουν αρχικές συνθήκες για τις οποίες η πέτρα απομακρύνεται συνεχώς από τη Γη. Η απάντηση είναι θετική.
Υπάρχει μια ελάχιστη ταχύτητα, την οποία αν αποκτήσει ένα σώμα στην επιφάνεια της Γης, δεν θα ξαναγυρίσει σε αυτή. Η ταχύτητα αυτή ονομάζεται
ταχύτητα διαφυγής (δεύτερη κοσμική ταχύτητα) και είναι ίση με
υδ = 11,2 km/s. Ενδεικτικά αναφέρουμε ότι η μέγιστη ταχύτητα που μπορεί να αποκτήσει ένα αγωνιστικό αυτοκίνητο Formula 1 στην κατάλληλη πίστα είναι περίπου
0,09 km/s, πολύ μικρότερη από αυτή που πρέπει να αποκτήσουμε αν θέλουμε να εγκαταλείψουμε τη Γη! Η ταχύτητα διαφυγής είναι ανεξάρτητη της μάζας του σώματος που ρίχνουμε. Εξαρτάται μόνο από τη μάζα της Γης και από την απόσταση του σώματος από το κέντρο μάζας της Γης.
- Ποιο το σχήμα της καμπύλης για διαφορετικές ταχύτητες ως προς την ταχύτητα διαφυγής;
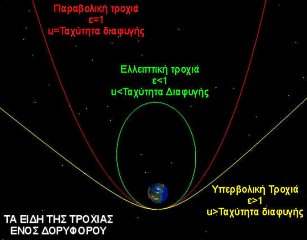 Αν η πέτρα αποκτήσει την ταχύτητα διαφυγής δεν θα ξαναγυρίσει πίσω και θα ακολουθήσει τροχιά
σχήματος παραβολής. Αν αποκτήσει ταχύτητα μεγαλύτερη από την ταχύτητα διαφυγής τότε αυτή θα απομακρυνθεί από τη Γη ακολουθώντας
υπερβολική τροχιά. Τέλος, αν η ταχύτητα είναι μικρότερη από τη
υδ τότε θα ακολουθήσει ελλειπτική τροχιά. Αν η πέτρα αποκτήσει την ταχύτητα διαφυγής δεν θα ξαναγυρίσει πίσω και θα ακολουθήσει τροχιά
σχήματος παραβολής. Αν αποκτήσει ταχύτητα μεγαλύτερη από την ταχύτητα διαφυγής τότε αυτή θα απομακρυνθεί από τη Γη ακολουθώντας
υπερβολική τροχιά. Τέλος, αν η ταχύτητα είναι μικρότερη από τη
υδ τότε θα ακολουθήσει ελλειπτική τροχιά.
- Σε ποια από τις παραπάνω περιπτώσεις θεωρούμε πως ένα σώμα είναι δορυφόρος της Γης;
Στην περίπτωση αυτή αναφερόμαστε συνήθως σε ελλειπτικές τροχιές οι οποίες έχουν την ιδιότητα να μην τέμνουν την επιφάνεια της Γης (είναι κλειστές ελλείψεις γύρω από τη Γη). Για να έχουμε τέτοιες κλειστές τροχιές πχ. γύρω από τη Γη και κοντά στην επιφάνεια της, πρέπει να ξεπεράσουμε την
πρώτη κοσμική ταχύτητα που έχει τιμή περίπου
8 km/sec. Η πρώτη κοσμική ταχύτητα ορίζεται για την επιφάνεια της Γης. Για μεγαλύτερα ύψη, η απαιτούμενη ταχύτητα για να παραμείνει ένα σώμα σε τροχιά είναι μικρότερη, καθώς η έλξη της Γης είναι ασθενέστερη. Κάθε σώμα που εκτοξεύεται από την επιφάνεια της Γης με μικρότερη ταχύτητα από την πρώτη κοσμική ταχύτητα πέφτει πάλι στη Γη διαγράφοντας ένα τμήμα έλλειψης.
B. Πως περιγράφουμε μια ελλειπτική τροχιά;
Οι τροχιές που μας ενδιαφέρουν και θα εξετάσουμε από εδώ και πέρα είναι οι ελλειπτικές. Για να περιγράψουμε μια ελλειπτική τροχιά χρησιμοποιούμε τα παρακάτω χαρακτηριστικά μεγέθη
(για διευκόλυνση, δείτε και τα σχετικά
σχήματα):
- Απόγειο (Α) είναι το σημείο της τροχιάς όπου η απόσταση του σώματος από τη Γη είναι η μέγιστη,
δηλαδή από τη μία εστία της έλλειψης όπου βρίσκεται η Γη. Αντίστοιχα για τη Σελήνη έχουμε το
αποκύνθιο.
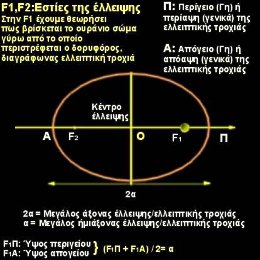 Περίγειο (Π) είναι το σημείο της τροχιάς που η απόσταση του σώματος από τη Γη είναι η ελάχιστη (το περίγειο και το απόγειο στην περίπτωση της ελλειπτικής τροχιάς βρίσκονται σε μια ευθεία που διέρχεται από τη Γη). Αντίστοιχα για τη Σελήνη έχουμε το
περικύνθιο. Περίγειο (Π) είναι το σημείο της τροχιάς που η απόσταση του σώματος από τη Γη είναι η ελάχιστη (το περίγειο και το απόγειο στην περίπτωση της ελλειπτικής τροχιάς βρίσκονται σε μια ευθεία που διέρχεται από τη Γη). Αντίστοιχα για τη Σελήνη έχουμε το
περικύνθιο.
- Μεγάλος ημιάξονας είναι το
μισό του ευθύγραμμου τμήματος που ενώνει το
απόγειο Α και το περίγειο Π μιας
ελλειπτικής τροχιάς. Σε μια
ελλειπτική τροχιά, το ουράνιο σώμα
γύρω από το οποίο γίνεται η
περιστροφή βρίσκεται τοποθετημένο
σε μια από τις δύο εστίες της
έλλειψης. Αν η εστία αυτή είναι η F1,
τότε το ύψος του απογείου είναι (F1A)
και του περιγείου (F1Π). Τότε
ισχύει: [(F1Α) + (F2Π)] = 2·α,
όπου α είναι το μήκος του μεγάλου
ημιάξονα.
- Εκκεντρότητα (ε) είναι το μέγεθος που μας δείχνει πόσο πεπλατυσμένη είναι η έλλειψη σε σχέση με τον κύκλο όπου έχουμε
ε = 0. Για το περίγειο, το απόγειο και την εκκεντρότητα, ισχύουν οι παρακάτω χρήσιμες σχέσεις:
(F1Α) = α · ( 1 + ε
) και (F1Π)
= α · ( 1 - ε )
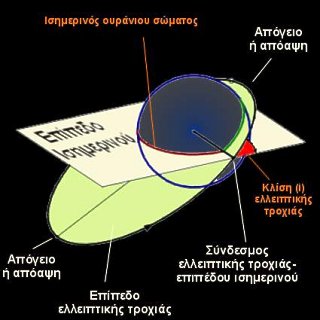 Επίπεδο
μιας ελλειπτικής τροχιάς είναι το επίπεδο πάνω στο οποίο βρίσκεται η τροχιά.
Στο σημαντικό συμπέρασμα πως κάθε τροχιά, γύρω από ένα
βαρύτικό πεδίο που προέρχεται από μια
μάζα (κεντρικό πεδίο) είναι επίπεδη,
καταλήγουμε με τη χρήση απλών
φυσικών νόμων. Επίπεδο
μιας ελλειπτικής τροχιάς είναι το επίπεδο πάνω στο οποίο βρίσκεται η τροχιά.
Στο σημαντικό συμπέρασμα πως κάθε τροχιά, γύρω από ένα
βαρύτικό πεδίο που προέρχεται από μια
μάζα (κεντρικό πεδίο) είναι επίπεδη,
καταλήγουμε με τη χρήση απλών
φυσικών νόμων.
- Κλίση μιας τροχιάς ως προς ένα επίπεδο είναι η
δίεδρη γωνιά που σχηματίζει το επίπεδο αυτό με το επίπεδο της τροχιάς του σώματος. Για τη Γη, την κλίση τη μετράμε ως προς το επίπεδο του ισημερινού της Γης.
- Περίοδος μιας τροχιάς είναι το χρονικό διάστημα που απαιτείται ώστε ο δορυφόρος να διαγράψει μία φορά την ελλειπτική τροχιά. Ισχύει:
- Σύνδεσμοι μιας τροχιάς με ένα επίπεδο είναι τα δύο σημεία τομής της τροχιάς και του επιπέδου αυτού.
Γ. Μεταβολές μιας ελλειπτικής τροχιάς
- Πως μεταβάλλεται η ταχύτητα ενός δορυφόρου που κινείται σε ελλειπτική τροχιά;
Η ταχύτητα του δορυφόρου σε κάθε σημείο της τροχιάς του δεν είναι σταθερή. Πρώτα απ' όλα αλλάζει η κατεύθυνσή της με τέτοιο τρόπο ώστε να παραμένει πάντα εφαπτόμενη στην τροχιά. Το μέτρο της δε είναι τέτοιο ώστε σε ίσους χρόνους να διαγράφει ίσα εμβαδά, όπως υπαγορεύει ο
2ος νόμος του Kepler. Έτσι, στο περίγειο το σώμα έχει τη μέγιστη δυνατή ταχύτητα και στο απόγειο την ελάχιστη.
- Με ποιο τρόπο μπορούμε να μεταβάλλουμε τα χαρακτηριστικά μιας ελλειπτικής τροχιάς;
Αν θέλουμε να μεταβάλλουμε τη μορφή της έλλειψης συνήθως αλλάζουμε την ταχύτητα του δορυφόρου στο περίγειο ή στο απόγειο. Τότε καταλήγουμε σε μία νέα ελλειπτική τροχιά η οποία το μόνο κοινό της σημείο με την αρχική είναι το σημείο όπου έγινε η μεταβολή της ταχύτητας.
- Πως μεταβάλλονται το περίγειο και το απόγειο μιας τροχιάς, αν γίνει μια μεταβολή στην ταχύτητα, σύμφωνα με τα όσα αναφέρονται στην προηγούμενη ερώτηση;
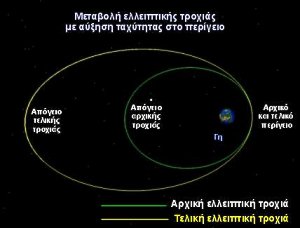 Για αύξηση ταχύτητας είτε στο περίγειο, είτε στο απόγειο, έχουμε αύξηση του ύψους του απογείου και του περιγείου αντίστοιχα. Για μείωση της ταχύτητας, το αποτέλεσμα είναι το αντίθετο. Οι υπολογισμοί για τα νέα ύψη απογείου ή περιγείου είναι εύκολοι με τη χρήση της αρχής διατήρησης της ενέργειας και της στροφορμής. Για αύξηση ταχύτητας είτε στο περίγειο, είτε στο απόγειο, έχουμε αύξηση του ύψους του απογείου και του περιγείου αντίστοιχα. Για μείωση της ταχύτητας, το αποτέλεσμα είναι το αντίθετο. Οι υπολογισμοί για τα νέα ύψη απογείου ή περιγείου είναι εύκολοι με τη χρήση της αρχής διατήρησης της ενέργειας και της στροφορμής.
- Πως μεταβάλλεται η περίοδος μιας ελλειπτικής τροχιάς, για αντίστοιχες μεταβολές στην ταχύτητα;
Αναφέρθηκε στην προηγούμενη ερώτηση πως με μεταβολή της ταχύτητας αλλάζει το ύψος του απογείου ή του περιγείου. Το ύψος του απογείου και του περιγείου καθορίζουν προφανώς την τιμή του μήκους του μεγάλου ημιάξονα
α. Όσο αυξάνει η ταχύτητα, το α αυξάνει και αντίθετα. Όμως, αναφέρθηκε πως η περίοδος εξαρτάται μόνο από το μήκος του μεγάλου ημιάξονα.
Αρα με αύξηση της ταχύτητας, η περίοδος της ελλειπτικής τροχιάς αυξάνει, ενώ με μείωση ο χρόνος της περιόδου μικραίνει.
Δ. Συνηθισμένα είδη ελλειπτικών τροχιών
Κάποια από τα είδη τροχιών που συναντώνται περισσότερο, ενώ πρόκειται να τα συναντήσουμε και στο
LunarSAT, είναι τα παρακάτω:
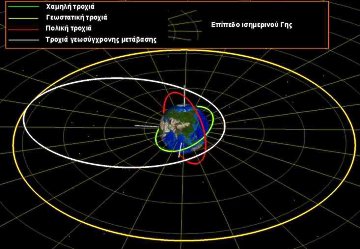 Χαμηλή ονομάζεται η τροχιά ενός δορυφόρου όταν αυτός κινείται σε ύψος μικρότερο από 4000 km από τη γήινη επιφάνεια. Μετά την εκτόξευσή του, το
LunarSAT θα εισέλθει σε χαμηλή τροχιά, από την οποία θα μεταβεί σε
τροχιά γεωσύγχρονης μετάβασης (βλέπε παρακάτω). Χαμηλή ονομάζεται η τροχιά ενός δορυφόρου όταν αυτός κινείται σε ύψος μικρότερο από 4000 km από τη γήινη επιφάνεια. Μετά την εκτόξευσή του, το
LunarSAT θα εισέλθει σε χαμηλή τροχιά, από την οποία θα μεταβεί σε
τροχιά γεωσύγχρονης μετάβασης (βλέπε παρακάτω).
- Ένας δορυφόρος που κατά την κίνησή του βρίσκεται συνεχώς πάνω από ένα συγκεκριμένο τόπο λέμε ότι κινείται σε
γεωστατική τροχιά. Δηλαδή η τροχιά του
είναι κυκλική, η κλίση της είναι μηδέν και η περίοδος της είναι ίση με την περίοδο περιστροφής της Γης (περίπου 24 ώρες).
- Τροχιά γεωσύγχρονης μετάβασης (GTO) ονομάζεται η ελλειπτική τροχιά ενός δορυφόρου γύρω από τη Γη, που το περίγειο της βρίσκεται σε μικρό σχετικά ύψος και το απόγειό της βρίσκεται στο ύψος της γεωστατικής τροχιάς, δηλαδή περίπου 36000 χλμ. από την επιφάνεια της Γης. Το
LunarSAT θα ξεκινήσει το ταξίδι του προς τη Σελήνη από μια
GTO
(Διευκρίνηση: η κλίση της GTO
δεν χρειάζεται να είναι μηδέν).
- Πολική ονομάζεται η τροχιά στην οποία ο δορυφόρος διέρχεται από τους πόλους του πλανήτη γύρω από τον οποίο κινείται και είναι προφανές ότι η κλίση της ελλειπτικής τροχιάς είναι
90°. Η τροχιά του LunarSAT γύρω από τη Σελήνη πρόκειται να είναι πολική
Τα παραπάνω στοιχεία αρκούν ώστε με μια ακολουθία σκέψεων και ιδεών που θα παρουσιάσουμε παρακάτω,
σε συνδυασμό και με ορισμένα στοιχεία
που θα αναφερθούν στο 2ο κεφάλαιο, να καταφέρουμε να εξηγήσουμε ποιοτικά την τροχιά του
LunarSAT. |


