2nd CHAPTER:
The Lagrange Points

A. Equilibrium Points

• What is a equilibrium point ?

Let's consider a body within the range of a force field. In case the ''source'' of this force is not a unique point in space, there might exist points where the total force that acts upon the body, disappears. These are called equilibrium points. So, if we put the body on this point with zero velocity, it will stay there forever. For example, between two masses, an equilibrium point always exists, in the position where the total gravitational force that originates from the one mass, is equal to the force that originates from the second.

• When an equilibrium point is considered stable and when unstable ?

Actually the question can be rephrased: If we place a body in an equilibrium point with zero velocity and we perturb it, what is going to happen? Well, that depends on the equilibrium point's properties. If it is stable, the perturbed body will oscillate back to the stability point. If it's unstable, the body will move away from the stability area gradually and will never come back.

B. The Lagrange Points

• What are the Lagrange points ?

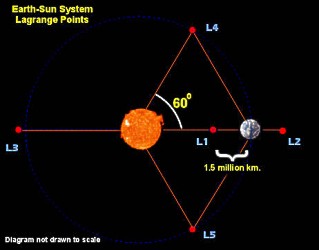Consider two masses. The one mass rotates on a circular orbit (or almost circular) around the second mass, which is not moving (e.g. the Earth rotating around the Sun). In this case, in relation to the line connecting these two masses, there are five fixed equilibrium points. These points are called Lagrange Points, after the French mathematician Joseph Louis Lagrange, who predicted their positions, after solving the so called "Three body problem" (the third body in this case is the satellite, which has very low mass in contrast to the other two masses). Three of the Lagrange points (L₁, L₂, L₃) lie upon the line connecting the two masses. The L₄ and L₅ points are placed 60^o forward and 60^o backwards on the orbiting mass's path, forming an equilateral triangle. On these points, the total force that acts on a mass is zero (be careful: not the total gravitational force).

• What are the properties of the Lagrange points ?

The L₁, L₂, L₃ points are unstable. That means that if a satellite is placed in any of these points, it should conduct corrective maneuvers in order to avoid being moved away by any kind of disturbing force (and there are many disturbing forces in real space). It should be noted that there is a stable orbit around each point. Although this is important, in the case of LunarSAT is useless, so we won't refer to it any more.

As for L₄ and L₅, they are stable. So the satellite that is placed in the area of any of these two points, will stay there forever. The most common example is that of the Trojan Asteroids. This group of asteroids lies on the L₄ and L₅ Lagrange points of the Sun - Jupiter system.

• What are the advantages of using the Lagrange points (or the areas surrounding them) in space missions ?

The fact that the Lagrange points are equilibrium points and because they hold a stable position in relation to the two celestial bodies, offer numerous options to space mission designers. Some of the most important are the following three:

( A ) The L₁ Lagrange point of the Sun - Earth system, lies on the line connecting these two bodies and between them. So, a spacecraft that is placed in the stable orbit around L1, could measure the solar wind's properties, and therefore notify the scientist's on the Earth about the upcoming solar activity. SOHO is an ESA - NASA satellite that does exactly these kinds of measurements.

( B ) All the Lagrange points of the Sun - Earth system are ideal (besides L₃) for placing large space telescopes. These positions offer continuous communication with the Earth and in addition, they apply for better observations. That's because any of the Sun - Earth Lagrange points is at least 1.5 million kilometers away from the Earth, so that our planet's volume doesn't block any part of the sky (like in the case of Hubble Space Telescope). Actually, the next great space telescope (Next Generation Space Telescope) is planned to be placed on a halo orbit around the L₂ point of the Earth - Sun system.

( C ) Because in the surrounding area of the Lagrange points, the total force acting on a mass is almost zero (and zero in the center), a satellite that passes through that area is subject to major changes on its orbit. Imagine yourself in a place where the gravitational attraction is extremely low (for example on the surface of an asteroid). You could send a rock thousands of kilometers away, using just the strength of your arm.

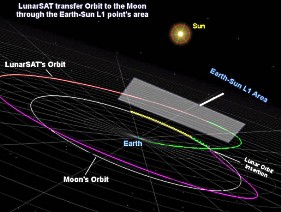
In a similar way, LunarSAT will modify its orbit in order to direct its way to the moon, by passing through the area of the Earth - Sun's L₁ point. To see exactly how and why this is going to happen, check the next chapter...