1st CHAPTER:
Basics of orbital mechanics

A. Introduction

• What is the escape velocity and in what does it depend on ?

If you throw a stone parallel to the ground, we can see that it's path describes a descending curve and after some time it meets the ground. The exact shape of that curve depends on the initial velocity. The question that arises is whether there is a velocity that if the rock is launched at this, it will never come back on Earth. The answer is yes.

There is a least speed that if a body has it at the ground level, it will never come back on Earth. This velocity is called escape velocity (second cosmic velocity), it doesn't depend on the direction the body is thrown (as long as it is not dropped with this velocity) and its magnitude is v_e=11,2 km/s. We give an example to show how great this velocity is: a racecar of Formula 1, in the proper circuit can achieve 0,09 km/s maximum speed. It is obvious that we need a much greater speed if we want to leave Earth forever! The escape velocity is independent of the body's mass. It depends only on Earth's mass and the distance between the body and the Earth's centroid.

• What is the shape of the path for velocities different to the escape velocity ?

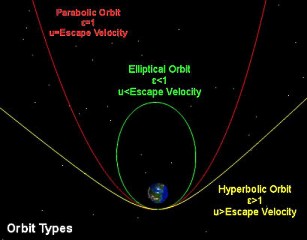If the stone is accelerated to the escape velocity, at ground level, its trajectory is parabolic. If its velocity is beyond the escape velocity, its trajectory is hyperbolic. Ending, if the launching velocity is less than the escape velocity, the stone's orbit will be elliptical.

• In which of the previous cases we consider the body as Earth's satellite ?

A body is Earth's satellite when its orbit is elliptical shaped and doesn't cross Earth's surface. The body will move in an elliptical orbit close to Earth's surface, only if its speed is greater than the first cosmic speed (v = 8 km/s). The first cosmic velocity refers to the ground level. In higher altitude the necessary velocity for a body to remain in orbit is lesser than 8 km/s because the gravitational attraction is weaker. Every body that is launched from Earth's surface with speed less than the first cosmic velocity, falls on the ground and its path is a part of an ellipse.

B. Elliptical Orbital Elements

The orbits we are interested in and we'll examine from now on are elliptical. To describe an elliptical orbit we use the following characteristic elements (see figures):

• Apoapsis (A) is the point of an elliptical orbit that is farthest away from the primary body. The center of the primary body is at one of the ellipse's [mathematical] focus points. If the system consists of Earth and the satellite, the apoapsis is called apogee. In moon-based systems, the apoapsis is called apolune.
   
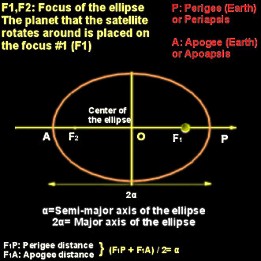• Periapsis (P) is the position in the orbit closest to the Earth. In Earth-based systems the periapsis is called perigee. (A line between perigee and apogee crosses Earth). In moon-based systems the periapsis is called perilune.
   
• Semi-major axis is one half the distance between apogee (A) and perigee (P). If the path is elliptical, then the body being orbited is at one of the ellipse's focus points. If this focus is called F₁, then the apogee's altitude is (F₁A) and the perigee's (F₁P). If a is the semi-major axis' length, then we have: [(F₁A) + (F₁P)] / 2 = a.
   
• Eccentricity (e) describes the shape of the elliptical orbit with respect to that of a circular that its eccentricity is zero. An eccentricity approaching one describes a highly elliptical orbit. Eccentricity is connected with apogee and perigee through the following equations:

(F₁A) = a · ( 1 + e ) and (F₁P) = a · ( 1 - e )

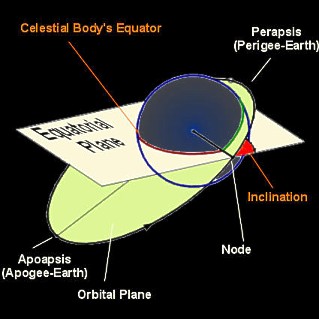• Plane of an elliptical orbit is the plane where the satellite is orbiting. Using simple laws of physics we end up in the useful conclusion that a body moving only due to the gravitational force of a planet, moves on a plane.
   
• Inclination is the angle between the planet's equator and the orbital plane.
   
• Period of an orbit is the time it takes to make a complete orbit.

• Nodes are the points in the equatorial plane that the orbit crosses.

C. Changing the elliptical orbit

• How the velocity of a satellite moving in an elliptical path is altered ?

The satellite's velocity is not constant in every position of the path. It is changing so as to remain tangential to the path. The velocity's magnitude is such so that a line between the center of the Earth and the satellite sweeps out equal areas in equal intervals of time (Kepler's Second Law). So, at the perigee the satellite moves fastest and at the apogee it moves slowest.

• How can we change the characteristics of an elliptical path ?

If we want to change the shape of the ellipse, we usually alter the satellite's speed at the perigee or at the apogee. Then the elliptical path is a new one and the only thing it has in common with the previous one is the position where we changed the speed.

• How perigee and apogee is changed, if the satellite gains or loses speed, according to the previous question ?

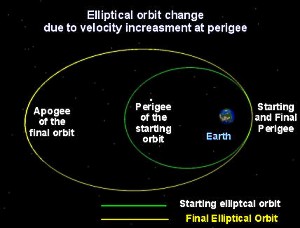If we increase the speed at the perigee or at the apogee, the apogee's and perigee's altitude will be raised. If we decrease the speed at the perigee or at the apogee, the apogee's and perigee's altitude will be lowered. We can easily calculate the new altitudes by using the conservation of energy and angular momentum.

• How will the period of an elliptical orbit change, if we alter the velocity ?

At the last question we referred to the way the apogee's and perigee's altitude will change, if the speed is altered. Those altitudes determine the length of the semi - major axis a. Speed and a are in proportion. As we have mentioned, period is a function of the semi - major axis' length a. So with the speed's increase, the period increases and when the satellite loses speed, the period reduces.

D. Types of Orbits

Some of the types of orbits that are commonly met and will be used by LunarSAT, too, are the following:

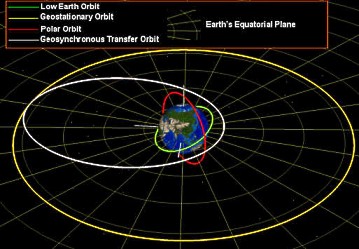• Low Earth orbit is called the orbit of a satellite that moves on an altitude lower than 4000 km from the Earth's surface. After its launch, LunarSAT will be launched into a low orbit and then into geosychronous transfer orbit (see below).
   
• Geostationary orbit is a circular orbit, its inclination is zero and the period is equal to the Earth's (approximately 24 hours). The satellite appears to remain above the Earth at a constant longitude.
   
• Geosynchronous transfer orbit (GTO) is the elliptical path with low perigee altitude and with an apogee altitude in the neighborhood of 36.000 km. LunarSAT will begin its journey from a GTO.
  (Clarification: GTO's inclination doesn't have to be zero).
   
• Polar orbit is a 90-degree inclination orbit (or almost 90) that covers both poles. LunarSAT's orbit around the Moon is going to be polar.

The above information are sufficient so that, in addition with some elements introduced in chapter 2, we will be able to describe and explain LunarSAT's orbit.